Hullspeed and the
Speed/Length Ratio

So what gives one boat better hullspeed than another? This question was pondered long and hard by William Froude (1810 to 1869), a British engineer who had a special fascination with the sea and ships.

Funded by the Admiralty, who were clearly very keen to get some answers to this question, he built a tank testing facility at Torquay, where he experimented with various model hull forms.

As an early expert in model analysis he was well acquainted with the 'law of mechanical similitude', which demonstrates among other things that there are few linear relationships in hull design.

So just what is the answer?

Let's take a look...

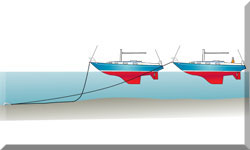
Hullspeed and the Matchbox Analogy

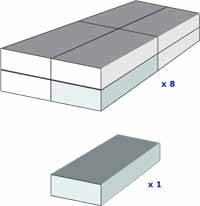The Matchbox Analogy

Consider your hull as a matchbox - not wonderfully efficient hydrodynamically, but stick with it for a moment.

Dissatisfied with the constraints of matchbox living, you decide to double its size. You add another matchbox ahead to double its length, two alongside to double its beam and four on top to double its draft.

Now wetted area has increased by four, volume and displacement by eight and stability - as the product of its mass and acceleration - has increased sixteenfold.

So by doubling a hull's dimensions, wetted area is squared, displacement is cubed and stability increases by the power of four.

With this knowledge and that gained by carefully measuring applied force and resultant movement, Froude was able to both calculate and demonstrate that a relationship existed between hull speed and waterline length - that relationship being known and described in the metric world as 'Froude Numbers'.

The Speed/Length Ratio

However, most of us more accustomed to units of feet and knots are probably more familiar with the Froude Number's close relation - the Speed/Length Ratio.

The Speed/Length Ratio

S/L Ratio = hullspeed (in knots) divided by the square root of the waterline length (in feet)

This discovery enabled Froude to compare the performance of boats of different length. For example a 25ft sailboat moving at 5 knots would have the same S/L Ratio at a 100ft patrol boat steaming along at 10knots, and consequently both would develop the same resistance per ton of displacement at those speeds.

For Froude's models, having no rig above the waterline to create windage, this resistance was caused by two principal factors; hull drag and wave making resistance.

Maximum Hull Speed

Maximum hull speed (in knots) = 1.34 x the square root of the waterline length (in feet)

Waterline Length

20 feet

25 feet

30 feet

35 feet

40 feet

45 feet

50 feet

Max Hull Speed

6.0 knots

6.7 knots

7.3 knots

7.9 knots

8.5 knots

9.0 knots

9.5 knots

These figures relate to a boat in displacement mode. If sufficient power can be applied to overcome hull drag and enable the boat to plane, then other criteria will affect ultimate hullspeed.